О параметрах двухполюсников.

Двухполюсник, в общем случае, представляет элемент, сопротивление которого может быть записано в виде комплексного выражения в алгебраической форме записи 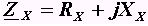. Здесь R_x и X_x соответственно резистивное и реактивное сопротивления двухполюсника.
Сопротивление двухполюсника может быть записано в виде комплексного выражения в показательной форме записи 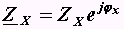. Здесь Z_x и j _x соответственно модуль и угол сопротивления двухполюсника. Они могут быть определены соответствующими выражениями: .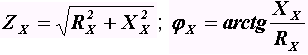
Добротность 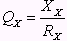и тангенс угла потерь 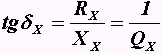являются обратными величинами.
Угол потерь и угол сопротивления двухполюсника в сумме дают прямой угол 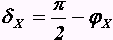. На векторной диаграмме представлены эти углы.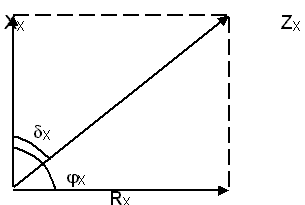

Методы измерения параметров двухполюсников на переменном токе

1. Мостовой метод получил широкое распространение благодаря высокой точности измерения. На рисунке представлена схема четырехплечего моста типа Уитстона

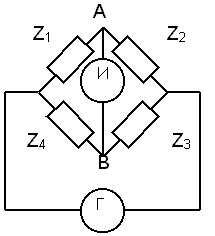
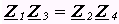В одну из диагоналей моста включают генератор Г, а в другую – индикатор И. Изменяя сопротивление плеч моста, можно добиться такого состояния схемы, когда индикатор покажет отсутствия тока в диагонали АВ моста. Мост в таком состоянии называют уравновешенным. Аналитически условие равновесия моста можно записать . В показательной форме 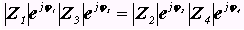. Равенство двух комплексных чисел возможно, если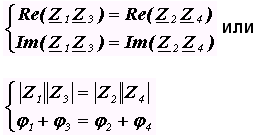

Эти выражения широко используют при анализе схем мостов.

Примеры схем мостов:
1. Дана схема моста. Выразить неизвестные элементы.

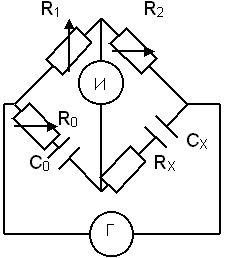
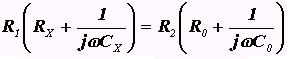В соответствии с условием равновесия моста запишем , откуда получим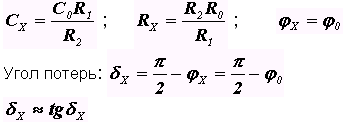

Это равенство справедливо до 10^о с погрешностью не менее 1%.

2. Надо разработать мост для измерения сопротивления индуктивного характера (желательно использовать образцовый конденсатор).
Схема может выглядеть так:

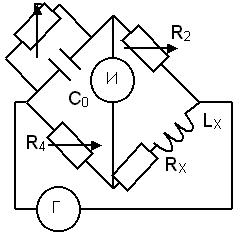
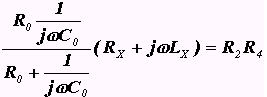В соответствии с условием равновесия моста запишем , откуда получим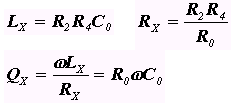

Недостатки мостового метода:
паразитные связи (емкостные, так как 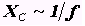, то с ростом частоты влияние паразитных связей возрастает).

Резонансный метод измерения параметров двухполюсников.

На частотах более 50кГц для измерения параметров двухполюсников применяют метод, в основе которого лежит явление резонанса. Схема такого метода представлена на рисунке.

G – генератор гармонических колебаний, перестраиваемый по частоте в широких пределах; L C₀ – измерительный контур;
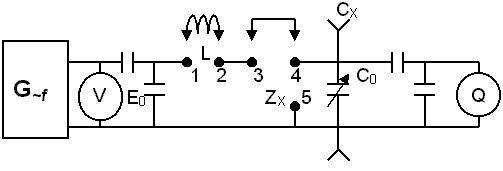
безымянные четыре емкости – емкостные делители напряжения, ослабляющие степень влияния генератора и вольтметров на измерительный контур.
В контуре можно достигнуть резонанса путем изменения емкости С₀ или частоты генератора.
После настройки на резонанс отношение напряжений на емкости или индуктивности к вводимому напряжению в контур примерно равно добротности.

Прибор прямо измеряет добротность, если напряжение Е₀ поддерживается постоянным. Такой прибор называют измерителем добротности или куметром.
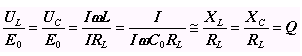
Резонансную частоту через элементы контура определяют:

Измеренное по идеальной характеристике – действительное значение катушки индуктивности.
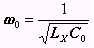
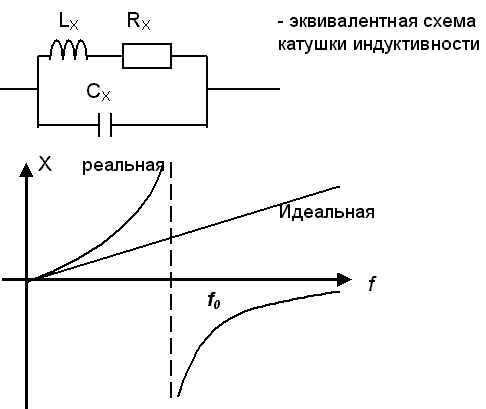
Измеренное по реальной характеристике – действующее значение катушки индуктивности.

Чтобы измерить С_L надо провести измерения на двух частотах

отсюда можно выразить

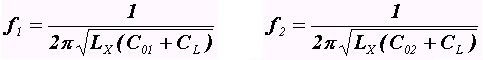
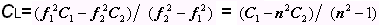
Измерения параметров двухполюсников измерителем добротности проводят в два этапа:
1. Измеряют параметры образцового резонанса контура, состоящего из встроенного в прибор образцового конденсатора и образцовой сменной катушки. Образцовую сменную катушку выбирают таким образом, чтобы частота, на которой будут выполнять измерения, попадала в диапазон частот, указанный на образцовой катушке. Настроив на заданной частоте образцовый контур в резонанс путем изменения образцовой емкости, снимают показания добротности и образцовой емкости, которые обозначим через Q₁ и С₁ .
2. В зависимости от величины модуля сопротивления, измеряемый объект включают параллельно или последовательно в образцовый контур. После этого, производят настройку образованного контура в резонанс на заданной частоте изменением образцовой емкости. Добротность контура и образцовую емкости обозначим через Q₂ и C₂ .
С помощью формул производят вычисления параметров измеряемого объекта.

Запишем выражения для первого этапа.
Зажимы 3-4 замкнуты, тогда сопротивление между точками 1-5 выразим 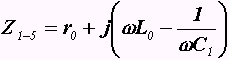, в момент резонанса ,

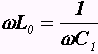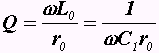
Запишем выражения для второго этапа.
В зажимы 3-4 включим Z_X, тогда сопротивление между точками 1-5 выразим
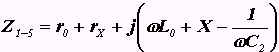
Из этих выражений можно вывести значение реактивной и резистивной составляющих сопротивлений. В момент резонанса выражение в скобках равно нулю, поэтому

Аналогично можно вывести формулы для параллельного подключения к контуру измеряемого объекта.

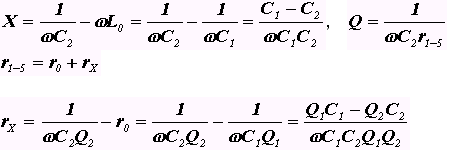
Резонансный метод измерения параметров двухполюсников можно характеризовать:
достоинства - простота, дешевизна;
недостатки - т.к. измерения проводятся на ВЧ, то велика погрешность измерения вольтметрами, неточность настройки в резонанс.