Тема 3. Погрешность измерений. Обработка результатов
Погрешность (неопределённость) - отклонение результата измерения Ах от истинного значения А. В международной практике рекомендовано применение термина неопределённость, в отечественной нормативной документации и учебной литературе преобладает использование термина погрешность.
D = Ax - A - формула погрешности, где:
A - истинное значение - значение, которое бы идеальным образом отражало в качественном и количественном отношениях измеряемую величину;
Ax – результат измерения. Так как истинное значение величина идеальная и, следовательно, неизвестная, то на практике вместо нее применяют действительное значение A0:
D = Ax - A0
A0 - действительное значение, найденное экспериментальным путем и настолько приближающееся к истинному, что для данной цели может быть использовано вместо него.
Классификация погрешностей.
5.1 аддитивные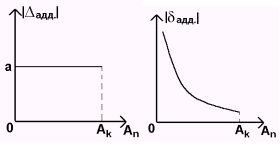 |
5.2 мультипликативные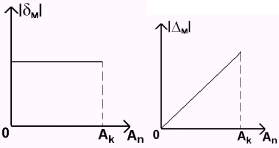 |
Ак – конечное значение диапазона измерения.
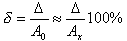
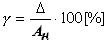
Относительную погрешность часто выражают в %. Для этого нужно на 100
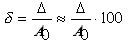
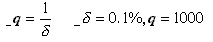
Инструментальную погрешность нормируют путем указания пределов допускаемой погрешности, которые указываются в метрологических характеристиках средства измерения.
D пред. – наибольшая по модулю погрешность средства измерения, при которой оно еще может быть допущено к применению. Фактически, это граница погрешности, за которую она не должна выходить. Таким образом, это позволяет определить границы, в которых находится истинное значение измеряемой величины A:
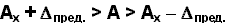 |
Пределы допускаемых погрешностей средств измерений могут быть указаны в метрологических характеристиках в разной форме:
- в форме абсолютной погрешности: класс точности обозначается M, N, O, R… или I, II, III…
- D пред. = a;
- D пред. = (a + вАк);
- D пред. = j (Ак),
j (Ак) - может быть задана формулой, отличной от формулы указанной в пункте 1.2, графиком или таблицей;
2. в форме относительной погрешности:
2.1 класс точности обозначен © , где с число из ряда: (1; 1,5; 2; 2,5; 4; 5; 5) × 10n , где n = 1, 0, -1, -2...
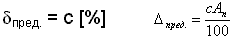 |
2.2 класс точности обозначен c / d – c и d числа из ряда, указанного в пункте 2.1;
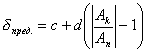 |
где Ак – наибольший по модулю из диапазонов измерения;
Аn – показания прибора
2.3 если класс точности обозначен, как в пункте 1, то d пред задается либо формулой, отличной от формулы указанной в пункте 2.2, либо графиком, либо таблицей;
3. в форме приведенной погрешности:
если класс точности обозначен,
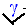 - число из ряда, указанного в пункте 1, то
- число из ряда, указанного в пункте 1, то  |
где: Ан – нормирующее значение, которое может быть равно:
а) Ан = Aк, если нулевая отметка находится на краю шкалы;
б) Ан = |Ak1| + |Ak2|, если нулевая отметка находится внутри рабочей части шкалы;
в) Ан = |Ak1| - |Ak2|, если нулевая отметка находится вне пределов шкалы (приборы с условным нулем), где Aк, Ak1 и Ak2 – конечные значения шкалы прибора. При измерении нужно стремится, чтобы показание прибора было как можно ближе к нормирующему значению. Вышеуказанные обозначения применяют для приборов с равномерной шкалой.
3.1 Для приборов с существенно неравномерной шкалой:
Обозначение:
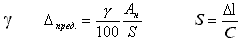 |
где Ан – нормирующее значение, равное геометрической длине всей шкалы приборов;
S – чувствительность приборов в точке отсчета показания;
Dl - размеры одного деления;
С – цена деления.
Случайная составляющая погрешности измерения (СлСПИ) и ее оценка.
Случайные погрешности исследуют и оценивают с помощью теории вероятности.
СлСПИ – погрешность изменяющаяся случайным образом, которая меняется при повторных измерениях случайным образом.
a1, a2, a3 … ai … an – ряд наблюдений,
n – число наблюдений,
ai – результат наблюдения (РН),
Случайная погрешность результата наблюдений: D i = ai - A
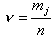 |
где mj – количество наблюдений, погрешность которых попала в j-ый интервал,
n - частота появления события.
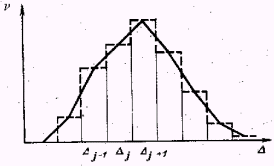
Гистограмма - зависимость частоты появления события от размера события. При предельном переходе гистограмма превращается в дифференциальный закон распределения плотности вероятности (правый график)
 |
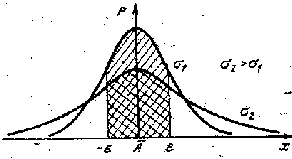 |
Чаще других встречается нормальный закон распределения случайных погешностей:
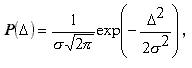
Нормальный закон распределения характеризуется двумя параметрами:
математическое ожидание M и среднеквадратическое отклонение s.
Введем новую переменную:
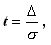
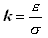 – нормированный доверительный интервал этой погрешности. После замены переменных получим следующее выражение
– нормированный доверительный интервал этой погрешности. После замены переменных получим следующее выражение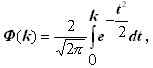
Алгоритм обработки РН при оценке СлСПИ.
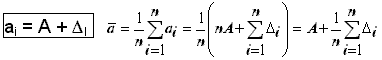
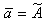 -
оценка результата измерения.
-
оценка результата измерения.- Вычислить оценку СКО РН:
а)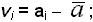
б)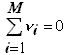 , если не равно 0, то нужно проверить верность выполнения п. 2;
, если не равно 0, то нужно проверить верность выполнения п. 2;
в)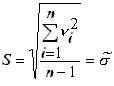 -
оценка среднеквадратичного отклонения;
-
оценка среднеквадратичного отклонения;
Нормальный закон пригоден для большого числа наблюдений, а как быть, когда число наблюдений мало? Прибегают к распределению Стьюдента :
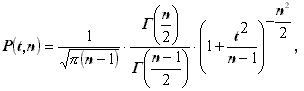
n – число наблюдений,
t – нормированная случайная погрешность среднего значения:
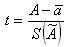
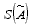 - оценка среднеквадратичного отклонения РИ.
- оценка среднеквадратичного отклонения РИ. 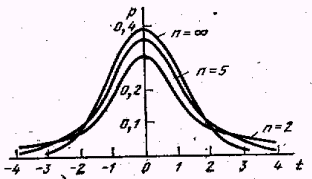
4. Вычислить оценку СКО РИ:
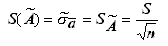
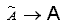
5. Проверка гипотезы о принадлежности к нормальному распределению;
а) n < 15 – невозможно определить;
б) 15 ³ n ³ 50 – определение по составному критерию ГОСТ 8.207-76;
в) n > 50 – определение по ГОСТ 11.06-74;
6. Выявление грубых погрешностей осуществляют в соответствии с ГОСТ 11.002-73, если есть анормальный результат наблюдения – его нужно исключить из ряда наблюдений и повторить вычисления с п. 2.;
7. Определить интервальные оценки СлСПИ:
а) задан доверительный интервал СлСПИ, Е – граница доверительного интервала. Вычисляют коэффициент Стьюдента ta
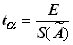
б) задана доверительная вероятность – P. С помощью таблицы распределения Стьюдента по известным P и n находят ta , а затем
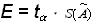 доверительный интервал СлСПРИ;
доверительный интервал СлСПРИ;8. Оформить результат измерения в соответствии с МИ 1317-86.
Систематическая составляющая погрешности измерения (СиСПИ) и ее оценка.
Классификация СиСПИ:
а) постоянная;
б) переменная.
Переменные:
Принципы исключения СиСПИ:
Оценка границ СиСПИ Q осуществляется по ГОСТ 8.207-76:
1. m > 3 (m – количество источников СиСПИ)
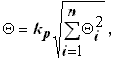
k – коэффициент, определяемый заданной вероятностью P
P |
0.9 |
0.95 |
0.98 |
0.99 |
kp |
0.95 |
1.1 |
1.3 |
1.4 |
2. m £ 3 Е
Если закон равномерный:
1. 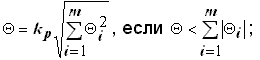
2. в противном случае 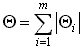 .
.
Из двух результатов берут меньший.
3. Если закон нормальный, то при любом m
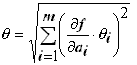
Опроеделение доверительных границ погрешности результата измерений ( ДГПРИ )
Определим ДГПРИ, если известно: Q ,
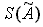 , P, E.
, P, E. Необходимо найти: D - ДГ суммы НРИ.
- если
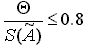 D
= E;
D
= E;- если
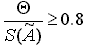 D
= Q
;
D
= Q
;- в остальных случаях D = k(E + Q ), где k – безразмерный коэффициент.
Границы Е и О должны быть определены с одинаковой вероятностью.
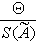 |
0.75 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| k(P = 0.95) |
0.77 |
0.74 | 0.71 | 0.73 | 0.76 | 0.78 | 0.79 | 0.8 | 0.81 |
| k(P = 0.99) |
0.85 |
0.82 | 0.8 | 0.81 | 0.82 | 0.83 | 0.83 | 0.84 | 0.85 |
Оценка погрешности косвенных измерений (РД50-555-85)
Пусть существует A = f(a1, a2 … am), где:
А – величина подвергаемая косвенному измерению,
a1, a2 … am – измеренные величины (прямые измерения).
- Исключим СиСПИ из результатов прямых измерений;
- Найдем
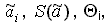
- Проверить степень корреляции аргумента.
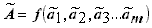 - оценка результата косвенного измерения;
- оценка результата косвенного измерения;- Вычислить оценку СКО случайной составляющей погрешности результата косвенного измерения
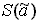
- Вычислить границу неисключенной СиСПРИ
где
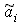 -
результат I-го измерения,
-
результат I-го измерения, 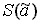 -
оценка СКО случайной составляющей, Q
I – границы неисключенной систематической составляющей;
-
оценка СКО случайной составляющей, Q
I – границы неисключенной систематической составляющей;Дальнейшая обработка справедлива только для слабо коррелированных величин.
а)
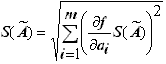
б) если нелинейная зависимость, то
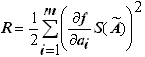 , (2);
, (2);в) если R ³ 0.8 ×
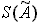 , то нужно ввести поправку:
, то нужно ввести поправку: 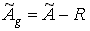 ;
;а) если m > 3 и закон распределения равномерный
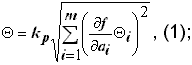 , (1);
, (1);б) если m £ 3, то рассчитывают по формуле (1) и по формуле
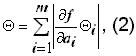 , (2)
, (2)из двух значений (1) и (2) выбирают меньшее.
Если закон распределения СиСПИ нормальный, то при любом m:
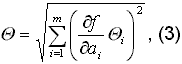
Если известны границы суммарной погрешности результатов прямых измерений D предi, и закон распределения, то для оценки нужно использовать формулу (3), где вместо Q i ставится D предi. ДГ суммы погрешностей РИ – см. выше.
- Результат эксперимента должен быть представлен с указанием единиц измерения;
- Обязательно должны быть указаны характеристики погрешностей измерения:
- указываются границы суммарной погрешности и доверительная вероятность, с которой погрешность находится в этих границах;
- отдельно указываются характеристики случайной и систематической составляющих погрешности. Причем могут быть указаны либо границы погрешности с указанием вероятности, либо статистические параметры распределения, т.е. оценка СКО и закон распределения (если есть возможность).
3. Погрешность измерения должна выражаться не более чем двумя значащими цифрами. Можно указать одну значащую цифру, ели погрешность округления не превышает 5 % (погрешность округляют в большую сторону). Если погрешность округления в большую сторону превышает 5%, то можно округлять в меньшую сторону до двух значащих цифр.
4. Критерий округления результата измерения:
последний разряд результата должен быть таким же, как у округленного значения абсолютной погрешности.
5. Результат измерения должен включать в себя условия проведения измерения (температура, давление, влажность, число наблюдений, частота, на которой проведены измерения, и т. п.).